It’s November 5, and like much of the country, I’ve been glued to the television all day, watching state election percentages swing from 49% to 50% and back again, pacing across the room, considering likelihoods of increasingly speculative scenarios, and agonizing over margins in Nevada and Pennsylvania.

Regardless of your political views, it’s obvious that this is an insanely nerve-wracking election with extreme consequences for the future of the U.S. and the world, and though I’m not afraid to get political and certainly will when the situation calls for it, I thought I’d write about something a little more unique today: the fairness of our electoral process and a fascinating mathematical process that could transform it for the better—if only we’d adopt it across the board.

Elections are certainly intrinsically tied with math; there definitely has not been a shortage of percentages and probabilities over the last two days. The idea I’m going to take you through, however, isn’t used for predicting results, and it actually isn’t even really numbers. And it has much more to do with congressional elections than presidential elections. But bear with me—this has the potential to transform the entirety of our election process by un-gerrymandering America.

Dating back to 1812, gerrymandering is the process of dividing a state into congressional districts in a way that gives an unfair advantage to some political party, by placing the areas that typically vote for that side so that they get majorities in far more districts than would be expected in a fair process. It’s become a constant, corrupt presence in our democracy ever since politician Elbridge Gerry signed a manipulated ‘salamander-shaped’ district into law (hence the name gerrymandering), and thanks to mathematicians, we now have a way to combat it.

Two years ago, at a math competition at MIT, I met Dr. Moon Duchin of Tufts University. Glowing with enthusiasm, Duchin presented an original idea in her keynote lecture, taking an abstract concept in geometry known as ‘random walks’ to tackle a problem politicians long found almost impossible: creating a method of redistricting that gives no advantage to any political party.

The question is so difficult because politicians are a part of every step of the redistricting process, and not only is it challenging to see the impact of the lobbying of all these separate interests, but the question presents itself as way more intricate than it originally appears.

Let me show you what I mean. We clearly want a redistricting plan that is fair, but what exactly does “fair” mean? Here’s a dilemma. What if we have a state that typically votes 60% red and 40% blue and we want to divide it into five districts?

One way that might seem “fair” is making sure each of the five districts contain about 60% of the population that typically votes red and 40% that typically votes blue. A closer look, however, reveals that red, as the majority, will win every single district, and blue won’t be represented in Congress at all! We’ll want, instead, a situation that somehow results in 60% red seats (3 seats) and 40% blue seats (2 seats). How do we go about that?

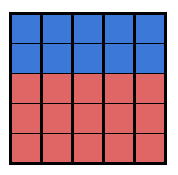
Depending on the arrangement of the population throughout the state, a solution could present itself easily. In our very simplified diagram, we could just divide the districts so that red remains with red and blue remains with blue:

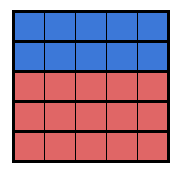
However, this solution is often not so easy to find, and it’s even very possible that the minority party can take the majority of the districts with the proper arrangement. (And, in fact, the more sections we define our region up into, the more possibilities there are for domination by either party regardless of which has the majority!)

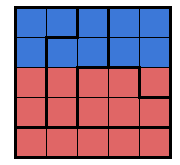
This is where Duchin comes in. Clearly, it is not ideal to have a group of congressmen (who benefit from particular redistricting plans) draw up the map, so why not have a computer do it? Duchin’s method not only removes human interests but also approaches the most equitable definition of fairness—all using a field of math known as geometric group theory in surprising new ways.

Geometric group theory is a very theoretical field, so abstract it lies essentially out of the realm of numbers. It takes surfaces and algebraic objects known as groups, and figures out what symmetries, geometries, and behaviors these complicated objects (often in higher dimensions!) harbor in their shapes. Many mathematicians explore these questions from purely a perspective of fascination for the beauty and aesthetics of these structures (which is why it’s often called “pure math”), and Duchin originally started her career here as well.

Her dissertation focused on taking ‘random walks’ across a particular class of surfaces with many twists along them, and seeing what happens if each time you take a “step” as you walk along the surface, you move and twist one of the sections, making the curve more and more complicated. She was interested in the long-term behavior, essentially what happens if you do this process for a very, very long time, and she found a way to represent this super complicated procedure but something much, much simpler in a smaller dimension.

This, of course, is extremely abstract, but there are many elements here that have already started to lend themselves to our question of redistricting. We’re taking something extremely complicated and making it simpler (just like taking a complicated map of areas that lean red or blue and placing them into just a few regions) and we’re watching long-term behavior (just like we may want to model districts over long periods of time).

For fear of losing you, I’ll step right back into the more practical question. Noticing a parallel between the often-bizarre shapes of gerrymandered congressional districts with the uber-complicated structures she works with in her theoretical career, Duchin began inventing a procedure for redistricting, noticing that what matters more is not the shapes of the districts but how they represent the people who live in them.

Our immediate criteria are that every district must have the same population and that they must be connected, and for the general purposes of redistricting, we should not divide up cities, counties, or communities that share a common interest unless we absolutely have to.

Our last condition is that we must actively work to represent minorities. Thinking back to the diagrams we had earlier, it’s actually most likely that we end up in a situation like Figure 1, where red takes every seat despite a significant portion of the population voting blue. Only by keeping minorities together (see Figure 2) do we give them a chance of maintaining the most equitable representation across the state. As long as that happens, the shapes don’t particularly matter.

This is the fundamental challenge: It’s very complicated to balance this idea of representing the minorities with the principle of majority rule. As Duchin found, if you randomly divide up the state into millions and millions of different ways, on average, you will be severely underrepresenting the minorities, and the extent to which you will completely depends on the geographic makeup of the state.

To quote Duchin, “there’s no reason to be confident that in the absence of partisan intent, 50-50 voting would lead to 50-50 representation. It’s just not necessarily the case. It depends on all this rich combination of these distributional, geometric, and combinatorial aspects.”

Even without lobbyists, it’s extremely difficult to find a plan that achieves the necessary proportions.

These are the large ideas that govern any initiative to un-gerrymander an area, and just so I don’t seem like I’m rambling, I’ll jump right into the important, mind-blowing results.

Duchin found that it is possible to generate a very equitable map, and it uses the very principles of random walks in geometric group theory that we just set aside as algebraic, theoretical knowledge that is only useful in its own right.

Twisting structures in higher dimensions can better our democracy. Think about that for a second. It’s completely crazy.

In 2018, the Pennsylvania government recruited Duchin. The Pennsylvania Supreme Court found that the redistricting plan was illegal, and unfairly favored the Republicans, so the governor brought her in to see if she could do something about it.

In a very broad sense, Duchin developed an algorithm that compares the set of all possible maps to a space relating to those bizarre mathematical structures. Next, it applies tons and tons of adjustments to these maps to make them more fair (similar to twists!). Then, the algorithm runs for an extended period of time until it approaches one map that most fairly meets the all-important criteria we listed above. Duchin also closely followed and incorporated all the needs and intricacies within Pennsylvania’s electorate, and that became Pennsylvania’s new map.

Thanks to Duchin, we have successfully un-gerrymandered Pennsylvania. So here’s my thought for you. It’s only a matter of time before we can do the same for the entire country. Fair congressional democracy (or at least some approximation of it) is right around the corner, and it takes theoretical mathematicians to get us there.

Election laws are always some of the most complicated to address in our country—after all, the people who make them are in office because they benefited from them, and there are so many more inequities (like the Electoral College)—but this concept gives us hope.

We can be hopeful that there is a future where districts are not unfairly drawn (whether intentionally or not), and the people’s opinions (all of us!) are actually shown in the bodies that govern us.

If you’ve read my opinion piece from long ago, this is what I mean when I say math is both beautiful and meaningful. It isn’t merely an intellectual pursuit mathematicians let themselves be lost in, but it also has the power to impact extremely complicated and un-intuitive questions (like how to fairly represent minorities in redistricting) even when it seems to lie outside of that.

Of course, I am by no means an expert, and Duchin’s work spans way more than I could ever go into in an article and probably even hope to understand, but I thought this was worth sharing, a point of awareness to the wider world of mathematically fighting for equity.

Feel free to check out this podcast about Dr. Moon Duchin or this article to learn more about her work. She’s a phenomenal personality, and she’s even leading lots of comprehensive workshops and events for others in academia to follow in her footsteps, progressing such important work by adding to the ranks of those involved in it.

Just for fun, here is my website. I already write lots of mathy articles for my online community, GLeaM (Girls Leading through Math), so maybe this is the start of a math column for The Blue & Gold as well.

For now, see if you can consider systematic inequities in our democracy—and if what actually determines nail-biting elections are the people themselves or merely the constructs that guide the ballots. And, don’t forget to hold onto your hat as the chaos of this week unfolds all around us.